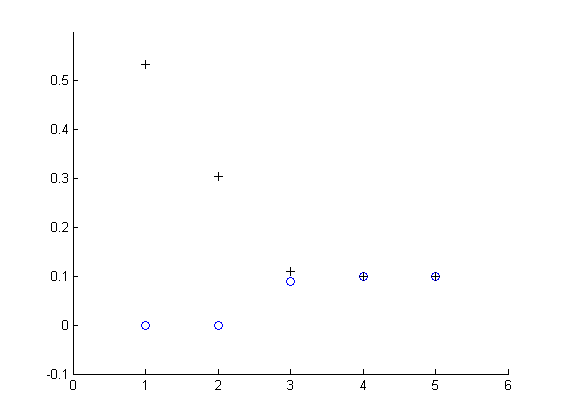
Tak už má někdo výsledek? Mně to vyšlo pro lambdu i epsilon: 0.1000. Nějak se mi i podařilo vykreslit ten graf. (Třetí pokus :) )

0.100 mi taky vyšlo (a zimmermann neprotestoval) - mickapa1

Má to někdo podobně? Nebo i úplně jinak? — Martin Zachar 2009/10/06 19:06

— mickapa1, ale nema to smysl porovnavat, zalezi asi i dost na inicializacni mnozine

Ano, lambda a epsilon mi vyšly stejně. Ta lambda na 0 na začátku není špatný nápad ;) — Roman Polášek 2009/10/07 12:04

Vcetne animace, jak algoritmus funguje, snad to nekterym pomuze v pochopeni. — Marek Sacha 2009/10/08 23:06

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Author: Marek Sacha <[email protected]> %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
clear
clc
close all
load data1.mat
 
% Initialize random set of starting active edges
% ix = vector of potential starting x-coordinates
ix = x(1);
% iy = vector of potential starting x-coordinates
iy = y(1);
 
% Initialize the point of maximum divergence (initial set contains only one point)
ixm = x(1);
iym = y(1);
 
% Initialize at, bt, lt
at = 0;
bt = 0;
lt = 0;
 
% Initialize totlerance
e = 0.0004;
 
% Initialize distance
dist = abs(at*ixm+bt-iym);
 
[ xh xw ] = size(x);
 
% Begin loop
while dist - lt > e
 
    test = dist - lt;
    % Get height of reduced vector x = height of reduced vector y, to be able
    % to constuct inequalities matrix for reduced problem
    [ ixh ixw ] = size(ix);
    % Construct inequalities matrix for reduced problem
    %       | ix   1  -1 |
    % A =   |-ix  -1  -1 |
    % 
    A = [ ix ones(ixh,1) -1*ones(ixh,1); -1*ix -1*ones(ixh,1) -1*ones(ixh,1) ];
    % Construct right side for reduced problem
    %     |  iy |
    % b = | -iy |
    b = [ iy; -iy ];
    % Construct function to be minimized
    % f = 0x + 0y + lambda
    f = [ 0; 0; 1];
    % Run linprog
    o = linprog(f,A,b);
    % o = [ at bt lambdat ];
    at = o(1);
    bt = o(2);
    lt = o(3);
 
    % Search for points of maximum distance (ixm, iym) and finally the maximum
    % distance
    max_dist = 0;
    for i=1:xh
        actual_dist = abs(at*x(i)+bt-y(i));
        max_point_x = [ x(i) ];
        max_point_y = [ y(i) ];
        if actual_dist > max_dist
            max_dist = actual_dist;
            imx = max_point_x;
            imy = max_point_y;
        elseif actual_dist == max_dist
            imx = [ max_points_x ; max_point_x ];
            imy = [ max_points_y ; max_point_y ];
        end
    end      
 
    dist = max_dist;
 
    if dist - lt > e
        ix = [ ix; imx ];
        iy = [ iy; imy ];
    end
 
    clf;
    hold on;
    % Print separate points
    plot(x,y,'y.');
    % Print separate points
    plot(ix,iy,'r.');
    % Approximation line
    plot(x,x*at+bt,'g');
    % Top border
    plot(x,x*at+bt+lt,'c');
    % Bottom border
    plot(x,x*at+bt-lt,'c');
    hold off;
 
    pause(2);
end
 
at
bt
lt

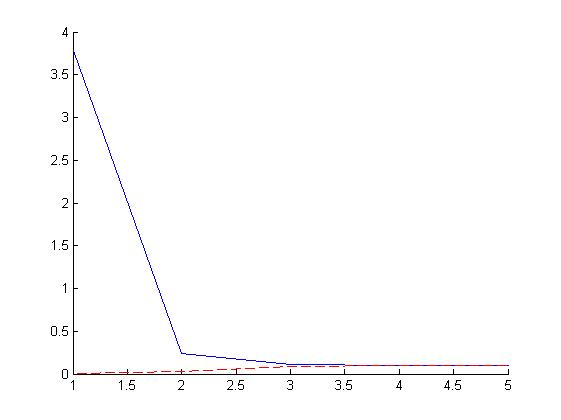
Konverguje v 5 krocich. — Marek Sacha 2009/10/08 23:06

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Author: Marek Sacha <[email protected]> %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
clear
clc
close all
load data2.mat
 
% Initialize random set of starting active edges
% ix = vector of potential starting x-coordinates
ix = x(1);
% iy = vector of potential starting x-coordinates
iy = y(1);
 
% Initialize the point of maximum divergence (initial set contains only one point and in fact, why not random number one ;-))
ixm = x(1);
iym = y(1);
 
% Initialize at, bt, lt
at = 0;
bt = 0;
lt = 0;
 
% Initialize totlerance
e = 0.0004;
 
% Initialize distance
dist = abs(at*ixm+bt-iym);
 
% Initialize support vectors for final graph
idist = [ dist ];
il = [ 0 ];
 
[ xh xw ] = size(x);
 
% Begin loop
while dist - lt > e
 
    test = dist - lt;
    % Get height of reduced vector x = height of reduced vector y, to be able
    % to constuct inequalities matrix for reduced problem
    [ ixh ixw ] = size(ix);
    % Construct inequalities matrix for reduced problem
    %       | ix   1  -1 |
    % A =   |-ix  -1  -1 |
    % 
    A = [ ix ones(ixh,1) -1*ones(ixh,1); -1*ix -1*ones(ixh,1) -1*ones(ixh,1) ];
    % Construct right side for reduced problem
    %     |  iy |
    % b = | -iy |
    b = [ iy; -iy ];
    % Construct function to be minimized
    % f = 0x + 0y + lambda
    f = [ 0; 0; 1];
    % Run linprog
    o = linprog(f,A,b);
    % o = [ at bt lambdat ];
    at = o(1);
    bt = o(2);
    lt = o(3);
 
    % Search for points of maximum distance (ixm, iym) and finally the maximum
    % distance
    max_dist = 0;
    for i=1:xh
        actual_dist = abs(at*x(i)+bt-y(i));
        max_point_x = [ x(i) ];
        max_point_y = [ y(i) ];
        if actual_dist > max_dist
            max_dist = actual_dist;
            imx = max_point_x;
            imy = max_point_y;
        elseif actual_dist == max_dist
            imx = [ max_points_x ; max_point_x ];
            imy = [ max_points_y ; max_point_y ];
        end
    end      
 
    dist = max_dist;
 
    if dist - lt > e
        ix = [ ix; imx ];
        iy = [ iy; imy ];
        idist = [ idist; dist ];
        il = [ il; lt ];
    else 
        idist = [ idist; dist ];
        il = [ il; lt ];
        % Hurray, we are victorious %
        clf;
        hold on;
        % Print actual distance
        plot(1:(ixh+1),idist,'yo');
        % Print lambda
        plot(1:(ixh+1),il,'r+');
        hold off;
 
        % Print out requested results
        dist
        lt
    end
 
end