Radiozita
Metoda pro řešení renderovací rovnice (výpočet globálního osvětlení), odvozená z Radiozity method (výpočet přenosu tepla)
původní článek: The radiosity method for diffuse environments (Goral et. al. 1984)
Dříve velmi populární metoda (jedna z prvních metod pro výpočet GI), vznikly o ní tisíce článků, dnes kromě okrajových případů považována za zastaralou
Princip
Aplikuje metodu konečných prvků (finite elements method) pro simulaci šíření světelné energie ve scéně
world-space metoda, pracuje přímo s povrchy scény, produkuje pohledově nezávislé řešení které lze rychle zobrazit z různých pohledů
Schéma klasické radiozity:
Omezíme popis scény - pouze difůzní materiály, difůzní uniformní plošné zdroje světla
Všechny povrchy ve scéně se rozdělí na malé polygony (typicky trojúhelníky) - patches. Každý patch má po celé ploše stejný materiál a stejné osvětlení.
Spočítáme form factory F pro všechny dvojice patchů. Form factor F_i,j je úměrný energii odražené z bodu na i, která dopadne na patch j.
Díky výše uvedeným zjednodušujícím podmínkám lze za přispění černé magie z renderovací rovnice (rekurzivní dvojný integrál) odvodit radiozitní rovnici:
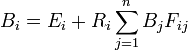
, kde B je radiosita (~osvětlení) patche a R je albedo (odrazivost, podíl dopadajícího světla na plošku který se odrazí). Radiosita plošky je tak jednoduše součet součinů ostatních radiosit a form factorů
Pro spočítání radiozity každé plošky máme 1 rovnici, dohromady nám pro n plošek dají soustavu n rovnic o n neznámých. Soustavu vyřešíme a dostaneme radiosity všech plošek ve scéně
Výsledky uložíme a vizualizujeme, například ray tracingem.
Problémy
omezení - pouze difůzní povrchy, světla, diskretizace na plošky - způsobuje chybu
diskretizace scény:
jak diskretizovat (hrubě: velká chyba, jemně: velká spotřeba paměti, doba výpočtu)
popis GI je závislý na scéně - nepodporuje libovolnou geometrii
form factory: je jich n^2, n je počet form factorů (těch jsou statisíce, miliony) - jak skladovat, jak počítat
řešení velké soustavy lineárních rovnic: naivní metody (gauss) nepoužitelné (O(n^3))
vizualizace: skoková změna osvětlení mezi ploškami působí rušivě
Řešení problémů
Existují (složité) způsoby jak omezení popisu scény obejít
adaptivní dělení (plochy blíž kameře/s velkou změnou osvětlení se dělí jemněji), discontinuity meshing (využívá se dodatečných znalostí o scéně pro dělení - například dělení podél stínů, atd).
Nepočítají se všechy form factory, jen relativně malý počet, ostatní se nastaví na 0. form factory se odhadují metodou Monte Carlo
Pro řešení soustavy rovnic se používají rychlé přibližné iterativní metody
Radiosita se interpoluje mezi sousedními ploškami, nebo se použije final gather (nastřílí se dotatečné paprsky z počítaného bodu, zprůměruje se výsledek)
Nahoru
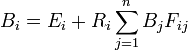 , kde B je radiosita (~osvětlení) patche a R je albedo (odrazivost, podíl dopadajícího světla na plošku který se odrazí). Radiosita plošky je tak jednoduše součet součinů ostatních radiosit a form factorů
, kde B je radiosita (~osvětlení) patche a R je albedo (odrazivost, podíl dopadajícího světla na plošku který se odrazí). Radiosita plošky je tak jednoduše součet součinů ostatních radiosit a form factorů