Toto je starší verze dokumentu!
Obsah
Popis algoritmu hledání minimální kostry orientovaného grafu
Právě se mi podařilo získat 6/10, tak snad už mám řešení a pochopení natolik dobré, abych se zde mohl podělit.
V dalším textu bude detailně popisován algoritmus sepsaný Ali Tofighem v Optimum Branchings and Spanning Aborescences (odkaz je na stránce úkolu - algorithm-description.pdf). Pokusím se popsat i optimální implementaci datových struktur. Nebudu zde opakovat to, co je z anglickém originálu naprosto jasné.
Datové struktury
Disjunktní množina
V algoritmu potřebujeme union-find množiny, které budou reprezentovat slabé a silné komponenty grafu a umožní nám snadno provádět jejich slučování. Strukturu je možné navrhnout například jako pole, kde index prvku odpovídá číslu vrcholu/komponenty a hodnota prvku odpovídá reprezentantu množiny. Funkce find pak vrací reprezentanta množiny, union slučuje dvě množiny. Je potřeba, aby find snižoval výšku stromu množiny. Snad jasné.
Binomická halda
Každý vrchol grafu si musí pamatovat množinu hran, které do něj vstupují. Z těchto hran bude vybírána vždy ta nejmenší. Dále bude potřeba umět dvě takovéto množiny efektivně sloučit (log n) a v konstantním! čase zvýšit váhu všech hran. Tohoto nejlépe docílíme právě upravenou binomickou haldou.
Nejtěžší je pravděpodobně zvyšování váhy všech hran v haldě. To lze provést tak, že přírůstek vah uložíme v prvním kroku jen do pomocné struktury haldy a dále tuto hodnotu šíříme haldou až v případě potřeby (odebírání vrcholu, slučování dvou hald). Každý uzel haldy si bude pamatovat kromě své váhy/klíče i přírůstek. Přitom je vhodné, aby platilo, že celková váha nějakého uzlu je součet přírůstků jeho rodičů (včetně té pomocné struktury haldy), jeho vlastního přírůstku a jeho původní váhy.
Propagace do nižších pater haldy probíhá vždy, když by se narušily správné celkové hodnoty vah uzlů. Jedním příkladem je odebírání minima z haldy. Pokud uzel minima obsahuje přírůstek, jeho pouhým odebráním bychom o něj přišli. Musíme tedy tento přírůstek propagovat do jeho potomků (o jedno patro níž). Další příklad je sloučení dvou hald. V takovém případě nemůžeme ponechat přírůstek v pomocné proměnné…atd. Doporučuju dobře otestovat, je to celkem fuška.
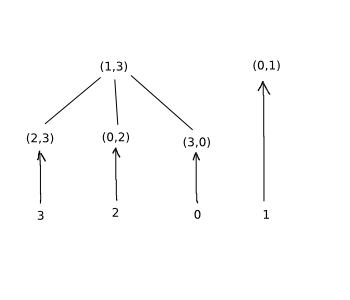
Les
Hrany s minimálními váhami, které budeme postupně vybírat si musíme někam ukládat, a to nejlépe tak, abychom nějakým snadným způsobem získali z této struktury výslednou minimální kostru. K tomuto účelu je potřeba připravit kořenový les, kde jednotlivými uzly lesa jsou hrany zadaného grafu. Je potřeba připravit se na to, že uzly které už v lese budou, bude občas potřeba přesunout v lese jinam - přesněji přidat je jako potomky jinému uzlu. A rozhodně není možné procházet les a hledat jestli v něm uzel (hrana grafu) náhodou už není :) Je potřeba konstantní čas.
Další lahůdkou je, že na konci algoritmu se bude les prořezávat. Budou se odstraňovat cesty (tedy uzly na cestě) vedoucí od nějakého listu lesa až do kořene, přičemž potomci odstraněných uzlů stoupají vzhůru (stávají se z nich kořeny lesa).
Osobně jsem implementoval les jako čtyřsměrně zřetězený spojový seznam (prev, next, parent, child).
Algoritmus
Následuje popis alg. v polopseudokódu :)
foreach (V as node) {
W.makeset(node); //na zacatku jsou vsechny uzly samostatnymi slabymi komponentami
S.makeset(node); //na zacatku jsou vsechny uzly samostatnymi silnymi komponentami
min[node] = node;
}
roots := V;
while ((r = roots.pop()) != NULL) {
/* vrati nejmensi hranu, pokud hrana smeruje z jedne silne komponenty do stejne silne komponenty,
zahodime ji a najdeme dalsi minimalni. Hrany tedy po nalezeni z haldy hned mazeme. Kdyz je halda
prazdna a zaroven uz mame ulozeny v "root" koren, znamena to, ze ma graf dva koreny a je tedy
neresitelny. Kdyz je halda prazdna a nemame jeste koren, ulozime ho (root = r;)
V originale je chybne osetreni korenoveho grafu - alg pak skonci pri zpracovani korenu (radek 14) a
nedoplni do lesa zbyvajici potrebne hrany. Je tedy potreba dale pokracovat dokud roots neni prazdne. */
edge = incoming[r].min();
u = edge.from;
v = edge.to;
/* pridani hrany do lesa. Druhy parametr je mnozina hran, ty se pridaji (presunou) jako potomci
hrany v lese. */
n = F.add(edge, cycle[r]);
if (cycle[r].isEmpty()) lambda[r] = &n; //lambda[r] je ukazatel na hranu v lese (vzdy ukazuje na list lesa)
if (W.find(u) != W.find(v)) { //uzly jeste nejsou nijak spojeny
W.union(W.find(u), W.find(v)); //spojime uzly do jedne slabe komponenty
enter[r] = edge; //poznacime jakou hranou se do uzlu dostavame - potrebne pro hledani cyklu dale
} else { //uzly uz jsou spojeny -> vznikl novy cyklus
/* ukladame hrany cyklu do C */
C.clear();
C.add(edge);
e = edge;
while (TRUE) {
e = enter[S.find(e.from)]; //dalsi hrana je hrana, kterou jsme se dostali do uzlu, z ktereho ted prichazime...
if (e == NULL) break;
C.add(e);
if (S.find(e.from) == S.find(edge.to)) break; //uz jsme v uzlu, z ktereho jsme vysli
}
max_edge = C.max(); //najdeme hranu s NEJVYSSI vahou
foreach(C as f) { //prochazime hrany cyklu a zvysujeme vahy hran vstupujicich do uzlu cyklu
k = S.find(f.to);
X.add(k); //seznam silnych komponent podilejicich se na cyklu
incoming[k].increase( max_edge.price - f.price );
}
/* cislo uzlu, ktery by se vybral jako koren, pokud bude tento superuzel vybran jako koren */
m = min[S.find(max_edge.to)];
S.union(X[i], X[i+1]); //proste sjednoceni vsech X, nenapada mne lepsi usporny zapis :)
rep = S.find(X[0]); //reprezentant celeho cyklu/superuzlu
min[rep] = m;
roots.push(repr);
cycle[r] = C;
/* slucujeme hrany vsech uzlu cyklu do jedne haldy. Vynechavani hran z Sr do Sr resit
nemusime, protoze to uz mame osetreno pri hledani nejlevnejsi hrany, kde je to imho vyhodnejsi */
incoming[repr].union(incoming[X[i]]); //X[i] != repr (nebudeme se slucovat sami se sebou)
}
}
/* v root nyni mame ulozene cislo uzlu, ktery pouzijeme jako koren kostry */
/* V lese existuje cesta smerujici do korene. Tu samozrejme nechceme a proto ji smazeme. */
if (lambda[min[root]] != NULL) {
F.delete_path_from(lambda[min[root]]);
}
while (!F.isEmpty()) {
e = F.get();
B.add(e); //pridame hranu do kostry
F.delete_path_from(lambda[e->to]);
}
/* v B mame hrany kostry */