Dva neprázdné binární stromy T1 a T2 prohlásíme za shodné, pokud levý podstrom kořene T1 je shodný s levým podstromem kořene T2 a zároveň pravý podstrom kořene T1 je shodný s pravým podstromem kořene T2. Každé dva prázdné binární stromy budeme pokládat za shodné (nebo, chcete-li, budeme uvažovat, že existuje jediný prázdný binární strom, který je shodný sám se sebou).

Máme k dispozici dvě operace, jimiž lze měnit tvar libovolného binárního stromu. První oprací je operace SWAP(x) představující výměnu levého podstromu libovolného uzlu x ve stromu s pravým podstromem tohoto uzlu x. Druhou operaci je operace ROTL(x) představující standardní levou rotaci v libovolném uzlu x tak, jak je známa pro AVL stromy.

Naším úkolem je aplikovat postupně dané operace na dané dva stromy tak, aby po jejich provedení byly oba stromy shodné. Operace lze provádět v libovolném pořadí a postupně vždy aplikovat na libovolný z obou zadaných a postupně se měnících stromů. Zároveň počet těchto operací musí být nejmenší možný.

Na vstupu jsou dva stromy, oba jsou zadány v identickém formátu. Strom je uveden řádkem s jediným celým číslem N označujícím počet uzlů ve stromu. Předpokládáme, že uzly stromu jsou očíslovány v neznámem pořadí čísly 1..N. Na dalších N−1 řádcích jsou uvedeny všechny hrany stromu, každá hrana je uvedena na jednom řádku. Hrana je specifikována dvojicí čísel A a B oddělených mezerou, kde A a B jsou čísla krajních uzlů hrany. Rodič má vždy nižší číslo než potomek. Pokud hrana vede z rodiče doleva, je uvedeno nejprve číslo potomka, pokud hrana vede z rodiče doprava je uvedeno nejprve číslo rodiče. Oba stromy na vstupu mají stejný počet uzlů.

Na výstupu je jediné číslo P uvádějící minimální počet daných operací, které je na dané stromy nutno aplikovat tak, aby vznikly dva shodné stromy. Není rozhodující, na které uzly kterého stromu a v jakém pořadí budou operace aplikovány.

Pozor, shodné stromy nemusí mít stejná čísla uzlů na odpovídajích si místech, shodnost je vlastností pouze tvaru stromu, nepočítá s obsahem nebo číslováním jednotlivých uzlů. Uzly stromů na vstupu jsou číslovány jen proto, aby byl snadno určitelný tvar stromů.

• 6
• 4 2
• 2 5
• 2 1
• 1 3
• 3 6
• 6
• 2 1
• 1 3
• 4 3
• 3 5
• 6 5

• 2

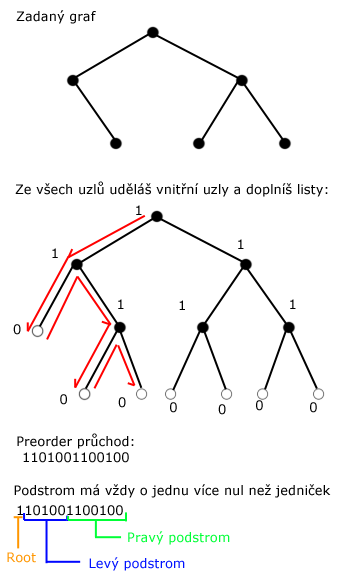
Reprezentace stromu, která se brala na cvičení s Berezovským:

EDIT BY KUBASTA

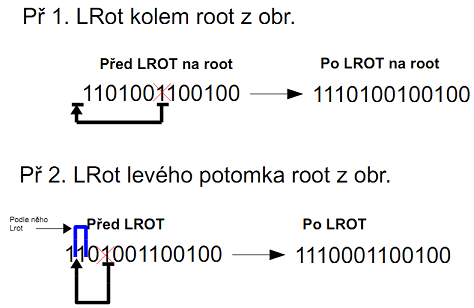
• BINARNI LROT

Binarni reprezentaci lze orotovat nasledujicim zpusobem:

• Pro dany vrchol najdi prvni uzel praveho podstromu
• Pokud je to 0, rotace nema smysl
• Pokud je 1, vyjmi ho bez nahrady a vloz ho pred (nebo za to je jedno) otce
• Pokud chces vsechny LROT udelej to pro vsechny 1 v reprezentaci stavu

• Príklady vztahujici se ke stromu vyse: